1.2 Центральное проецирование

Для перехода от пространственного представления о предмете к его плоскому изображению используется метод проекций.

Для того чтобы трехмерный объект, находящийся в трехмерном пространстве, «перенести» на плоскость, т. е. получить его изображение, необходимо его спроецировать. Для этого, из выбранной определённым образом точки пространства, которая называется центром проекции, необходимо провести прямые линии (лучи) через каждую точку изображаемого объекта. Эти прямые называются проецирующими прямыми. Та плоскость, на которой мы получили изображение предмета называется плоскостью проекции, а изображение предмета, которое мы получим на этой плоскости называется его проекцией.

В зависимости от положения центра проецирования и направления проецирующих лучей по отношению к плоскости проекций проецирование может быть либо центральным (коническим), либо параллельным (цилиндрическим).

Наиболее общий случай получения проекций пространственных фигур — это центральное проецирование.

В этом случае проецирующие лучи выходят из одной точки — центра проецирования S, который находится на конечном расстоянии от плоскости проекций П₁.

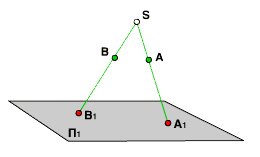
Для того чтобы получить центральные проекции точек А и B, необходимо провести проецирующие лучи из центра проецирования S через точки А и B до пересечения с плоскостью проекций П₁. При пересечении получаются точки А₁ и B₁ — центральные проекции точек А и B.

Положение точки S и плоскости П₁, которая не проходит через центр проекций, определяют аппарат центрального проецирования. Если он задан, то всегда можно определить положение центральной проекции любой точки пространства на плоскость проекции, при этом каждая точка пространства будет иметь только одну центральную проекцию. Однако, по одной центральной проекции невозможно определить положение точки в пространстве, так как она может находиться в любом месте прямой, соединяющей проекцию точки и центр проецирования.

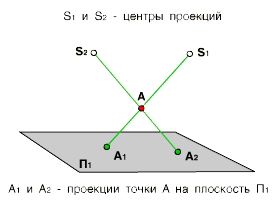
Для того чтобы определить положение точки А в пространстве по её центральным проекциям, необходимо иметь две центральные проекции этой точки А₁ и А₂, полученные из двух различных центров S₁ и S₂. Если провести проецирующие лучи S₁А₁ и S₂А₂, то точка их пересечения однозначно определит положение точки А в пространстве.

Для построения центральной проекции A₁B₁ отрезка АВ достаточно построить центральные проекции А₁ и B₁ точек А и В, так как две точки однозначно определяют прямую.

Центральное проецирование обладает большой наглядностью, так как оно соответствует зрительному восприятию предметов.

Свойства проекций при центральном проецировании:

1. Проекцией точки является точка.
2. Проекцией линии является линия.
3. Проекцией прямой в общем случае является прямая. (Если прямая совпадает с проецирующим лучом, то её проекцией является точка).
4. Если точка принадлежит линии, то проекция точки принадлежит проекции линии.
5. Точка пересечения линий проецируется в точку пересечения проекций этих линий.
6. В общем случае плоский многогранник проецируется в многогранник с тем же числом вершин.
7. Проекцией взаимно параллельных прямых является пучок прямых.
8. Если плоская фигура параллельна плоскости проекций, то её проекция подобна этой фигуре.